When ranking the strength of characters the natural thing to go by first is physics. However, since infinite force and energy is the highest degree of strength that a character can reach in terms of physics there would be no level of power above what is necessary to destroy an infinite universe, i.e. High 3-A.
Hence, in order to distinguish between the power of characters that are portrayed superior to that kind of power, we use a concept aside from physical strength: The concept of size.
The simple idea is that characters who can destroy much larger structures than others are likely also more powerful than them.
Dimensions are strongly related to the notion of size, as higher dimensional objects can be viewed as being infinitely larger than lower dimensional ones. Hence we use them as levels of power in our tiering system.
Note that while we use dimensions as the main measuring stick, we don’t ignore superior power of other nature. If a power has the necessary qualitative superiority over a certain level it can justify corresponding higher rankings in the tiering system. For more detailed information see Composite Hierarchies.
Intuitive Explanation[]
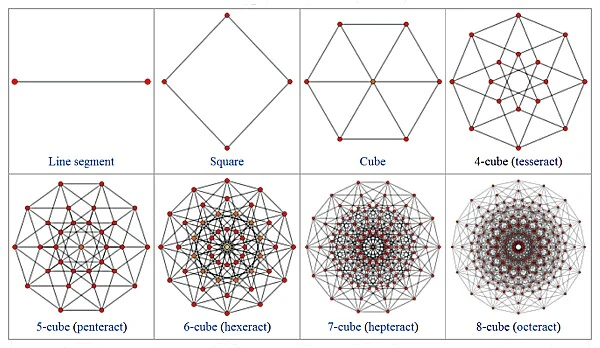
One easy way to envision the difference between dimensions is to envision it like the difference between a human and a (living) drawing of a human on an infinitely flat piece of paper. While we can move in 3 directions (upwards/downwards, left/right, forwards/backwards) the drawing can only move on the surface of the paper it is drawn on (only upwards/downwards and left/right). The infinitely flat piece of paper could be folded up to take up practically no volume and hence destroying it would mean destruction of a volume less than that of any 3-D object.
One can easily see the size difference if one looks at simple structures in different dimensions:
In 1-D everything is like a line. A line has only a length, but no width.
In 2-D there are planes, like for example squares. A square has a length and a width. If we talk about size in 2 dimensions we refer to area. However the area of a line is 0, because its area would be given by width x length, but its width is 0 and due to that also the area independent on what its length is.
3-D space is the space we usually live in. Size in 3-D space means volume. The difference between a 3-D and a 2-D object is like the difference between a 2-D and a 1-D object: A square has 0 height and its volume would be given by width x length x height. Because its height is 0 so is its volume, meaning that it is insignificantly small compared to the size of 3-D objects.
In a similar manner we can continue for all other dimensions, even if we can not imagine them anymore.
In 4 dimensions we, for example, would add an additional direction of extension beyond length, width and height. In this fourth direction the extend of a cube would be 0, so its 4 dimensional size, which would be height x length x width x fourth direction would always equal 0.
Here you can find an illustrated explanation, which treats the 4th dimension as time, as it is often done.
A menger sponge is also a good example to illustrate the case.
Mathematical Explanation[]
In order to understand the size difference between different dimensions, we first have to understand how size is quantified in mathematics. In order to do that we need to define various mathematical structures. Prerequisite for understanding the following is knowledge about what the terms function, set, subset, power set, union, intersection and complement mean in a mathematical context.
Note that the following explanations are informal and simplified.
σ-Algebra[]
If we want to deal with size mathematically, what we want to do is to assign a subset of some set S (which is our space) a number that quantifies its size. That means we want to define a function that projects from the power set of S unto a non-negative real number or infinite.
However, one can show that for size quantifications, that match our intuitive understanding of size, there is no such function if one really wants to define the function on the entire power set. Hence the function is instead only defined on a certain subset of the power set, the elements of which are called the measurable sets. But instead of choosing just some random subset of the power set we want that subset to be sufficiently rich in sets to properly work with it. This motivates the definition of a σ-Algebra:
Let S be a set and A be some subset of the power set of S. U is called a σ-Algebra if:
1. S is in A.
2. If some U is in A also S\U is in A.
3. If for any, up to countably infinite many, sets in A also the unification of the sets is in A.
Measure[]
A measure is the aforementioned function that projects the subsets of S, or more specifically the sets in the σ-Algebra A of choice, unto the non-negative real number that represents their size (or unto infinite).
A measure has to have to following properties:
1. The size of the empty set is 0. Or intuitively spoken the size of nothing is 0.
2. The size of the unification of up to countably infinite disjoint sets in A is equal to the sum of their individual sizes. That means intuitively spoken nothing, but that if one puts multiple separate objects together the size of the resulting object is equal to the sum of the sizes of the objects it was created from.
As one can guess from how general these properties are, there are many different measures on many different σ-Algebra and most of them don't classify what we imagine under a volume, even if they give something similar to a size. Hence we have to further specify which measure we want to use if we talk about size.
The Hausdorff measures[]
In order to have a measure that quantifies our understanding of size we wish to demand two more things than just basic measure properties. This things are:
- The n-dimensional size of an n-dimensional cube with side length 1 equals 1.
- Moving or rotating something doesn't change its size.
Some measures that fulfill this properties are the n-dimensional Hausdorff measures, if defined on the fitting Borel-Algebra. The Borel-Algebra is the σ-Algebra one gets by starting with all open subsets in the n-dimensional real coordinate space (or all closed sets, compact sets or half-open cubes) and adding in all sets necessary to make it a σ-Algebra. This Algebra is sufficiently extensive to quantify the size of pretty much any real life object.
Hausdorff measures have another property which makes them size wise intuitive.
An m-dimensional submanifold is a smooth lower-dimensional object that is within an higher-dimensional space. If one applies the m-dimensional Hausdorff measure to a submanifold it gives the correct sense of size. That means that for example the surface of a sphere in 3-D space would get its area as size if measured via the Hausdorff-measure.
Hausdorff dimension[]
How to classify the dimension of subsets of higher dimensional space is no easy question.
However one elegant solution comes due to the fact that, as priorly suggested, one can apply a lower-dimensional Hausdorff measure unto a subset of a higher-dimensional space (for example a submanifold).
Using this the Hausdorff dimension is defined as follows:
"The Hausdorff dimension of some subset of the n-dimensional real coordinate space (where n is some arbitrary natural number) is the lowest number d so that for all d', that are greater than d, the d'-dimensional size of the set (using the Hausdorff measure) is 0."
Or equivalently:
"The Hausdorff dimension of some subset of the n-dimensional real coordinate space (where n is some arbitrary natural number) is the highest number d so that for all d', that are smaller than d, the d'-dimensional size of the set (using the Hausdorff measure) is infinite."
In easier terms the dimension of an object is chosen so that from any lower dimensional perspective it appears infinite and from any higher dimensional perspective it appears to have 0 size.
This dimension term does match what one would expect the dimension of objects to be, for example the Hausdorff dimension of the surface of a sphere is 2 and the Hausdorff dimension of a cube is 3.
One interesting thing to consider if one wishes to get a sense on how large the difference between dimensions could be is the following:
Measures have the property that if one puts up to countably infinite separate objects together the size of the resulting object is equal to the sum of the sizes of the objects it was created from.
That means that the size of countably infinite objects of 0 size together have the size 0.
According to the first version of the definition of the Hausdorff dimensions one easily sees that the dimension of the unification of countably infinite n-dimensional objects is also a n-dimensional object. Or in other words stacking countably infinite objects together never reaches a higher dimension.